Class 10 Maths MCQs Chapter 8 Introduction to Trigonometry
1. The value of cos 0°. cos 1°. cos 2°. cos 3°… cos 89° cos 90° is
(a) 1
(b) -1
(c) 0
(d)
Answer
2. If x tan 45° sin 30° = cos 30° tan 30°, then x is equal to
(a) √3
(b)
(c)
(d) 1
Answer
3. If x and y are complementary angles, then
(a) sin x = sin y
(b) tan x = tan y
(c) cos x = cos y
(d) sec x = cosec y
Answer
4. sin 2B = 2 sin B is true when B is equal to
(a) 90°
(b) 60°
(c) 30°
(d) 0°
Answer
5. If A, B and C are interior angles of a ΔABC then 
Answer
6. If A and (2A – 45°) are acute angles such that sin A = cos (2A – 45°), then tan A is equal to
(a) 0
(b)
(c) 1
(d) √3
Answer
7. If y sin 45° cos 45° = tan2 45° – cos2 30°, then y = …
(a) –
(b)
(c) -2
(d) 2
Answer
8. If sin θ + sin² θ = 1, then cos² θ + cos4 θ = ..
(a) -1
(b) 0
(c) 1
(d) 2
Answer
9. 5 tan² A – 5 sec² A + 1 is equal to
(a) 6
(6) -5
(c) 1
(d) -4
Answer
10. If sec A + tan A = x, then sec A =
Answer
11. If sec A + tan A = x, then tan A =
Answer
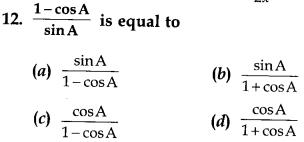
Answer
13. If x = a cos 0 and y = b sin 0, then b2x2 + a2y2 =
(a) ab
(b) b² + a²
(c) a²b²
(d) a4b4
Answer
14. What is the maximum value of
(a) 0
(b) 1
(c)
(d) 2
Answer
15. What is the minimum value of sin A, 0 ≤ A ≤ 90°
(a) -1
(b) 0
(c) 1
(d)
Answer
16. What is the minimum value of cos θ, 0 ≤ θ ≤ 90°
(a) -1
(b) 0
(c) 1
(d)
Answer
17. Given that sin θ = 
Answer
18. If cos 9A = sin A and 9A < 90°, then the value of tan 5A is
(a) 0
(b) 1
(c)
(d) √3
Answer
19. If in ΔABC, ∠C = 90°, then sin (A + B) =
(a) 0
(b) 1/2
(c)
(d) 1
Answer
20. If sin A – cos A = 0, then the value of sin4 A + cos4 A is
(a) 2
(b) 1
(c)
(d)
Answer
21. Ratios of sides of a right triangle with respect to its acute angles are known as
(a) trigonometric identities
(b) trigonometry
(c) trigonometric ratios of the angles
(d) none of these
Answer/Explanation
22. If tan θ = 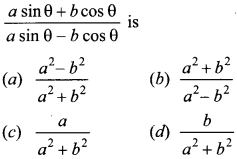
Answer/Explanation
23. Match the Columns:
(a) 1 – A, 2 – C, 3 – B
(b) 1 – B, 2 – C, 3 – A
(c) 1 – B, 2 – C, 3 – D
(d) 1 – D, 2 – B, 3 – A
Answer/Explanation
24. In the given figure, if AB = 14 cm, then the value of tan B is: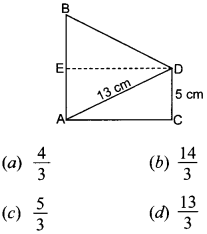
Answer/Explanation
25. Match the Columns:
(a) 1 – A, 2 – C, 3 – B
(b) 1 – C, 2 – A, 3 – D
(c) 1 – B, 2 – A, 3 – E
(d) 1 – B, 2 – D, 3 – A
Answer/Explanation
26. The value of sin² 30° – cos² 30° is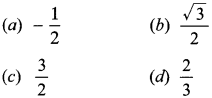
Answer/Explanation
27. If 3 cot θ = 2, then the value of tan θ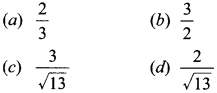
Answer/Explanation
28. If ∆ABC is right angled at C, then the value of cos (A + B) is [NCERT Exemplar Problems]
Answer/Explanation
29. If 0° < θ < 90°, then sec 0 is (a) >1
(b) < 1
(c) =1
(d) 0
Answer/Explanation
30. If sin 0 = √3 cos θ, 0° < θ < 90°, then θ is equal to
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer/Explanation
31. If cos (α + β) = 0, then sin (α – β) can be reduced to [NCERT Exemplar Problems]
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α
Answer/Explanation
32. If cos 9α = sin a and 9α < 90°, then the value of tan 5α is [NCERT Exemplar Problems]
(a)
(b) √3
(c) 1
(d) 0
Answer/Explanation
33. sin (45° + θ) – cos (45° – θ) is equal to
(a) 2 cos θ
(b) 0
(c) 2 sin θ
(d) 1
Answer/Explanation
34. The value of sin² 5° + sin² 10° + sin² 15° + … + sin² 90° is equal to
(a) 8
(b) 8.5
(c) 9
(d) 9.5
Answer/Explanation
35. The value of the expression [cosec (75° + θ) – sec (15° – θ) – tan (55° + θ) + cot (35° – θ)] is [NCERT Exemplar Problems]
(a) -1
(b) 0
(c) 1
(d)
Answer/Explanation
36. sin (90° – A) =
(a) sin A
(b) tan A
(c) cos A
(d) cosec A
Answer
37. tan A =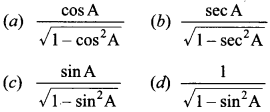
Answer/Explanation
38. If cosec A – cot A = —, then cosec A =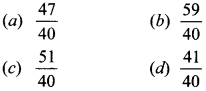
Answer/Explanation
39. If sin x + cosec x = 2, then sin19x + cosec20x =
(a) 219
(b) 220
(c) 2
(d) 239
Answer/Explanation
40. If sin θ – cos θ = 0, then the value of (sin4 θ + cos4 θ) is
Answer/Explanation
41. sec A =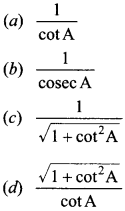
Answer/Explanation
42. 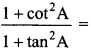
(a) tan² A
(b) sec² A
(c) cosec² A – 1
(d) 1 – sin² A
Answer/Explanation
43. If sec A + tan A = x, then tan A =






0 Comments